题目描述:
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入:
[10,9,2,5,3,7,101,18]
输出:
4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到O(n logn)吗?
一、动态规划: 注意: dp容器每个元素对应的数值表示以nums容器中对应的元素为尾数所能组成的最长上升子序列的长度; 比如:dp[3] = 2,则 dp[3] 对应于 nums 容器中的nums[3] = 5,即以5为尾数时,所能够组成的最长上升子序列(2,5)的长度为2(即dp[3]的值), 演示动画大致如下: 二、二分查找+贪心 这里需要说的是:这个辅助数组里面储存的不一定是题目要求的最长上升子序列,但是该辅助数组所储存的序列肯定是递增的,并且序列的长度,肯定是等于题目要求的最长上升子序列的长度 以上是我个人对这道题目的理解,不足之处请谅解,并欢迎指出错误,这将是提升自我的最大帮助!如果此文能够帮助到您,也烦请您点个赞收藏一下,鼓励鼓励在下
解题思路:
第一步:
新建一个容量大小与nums一致的容器dp,初始化为1
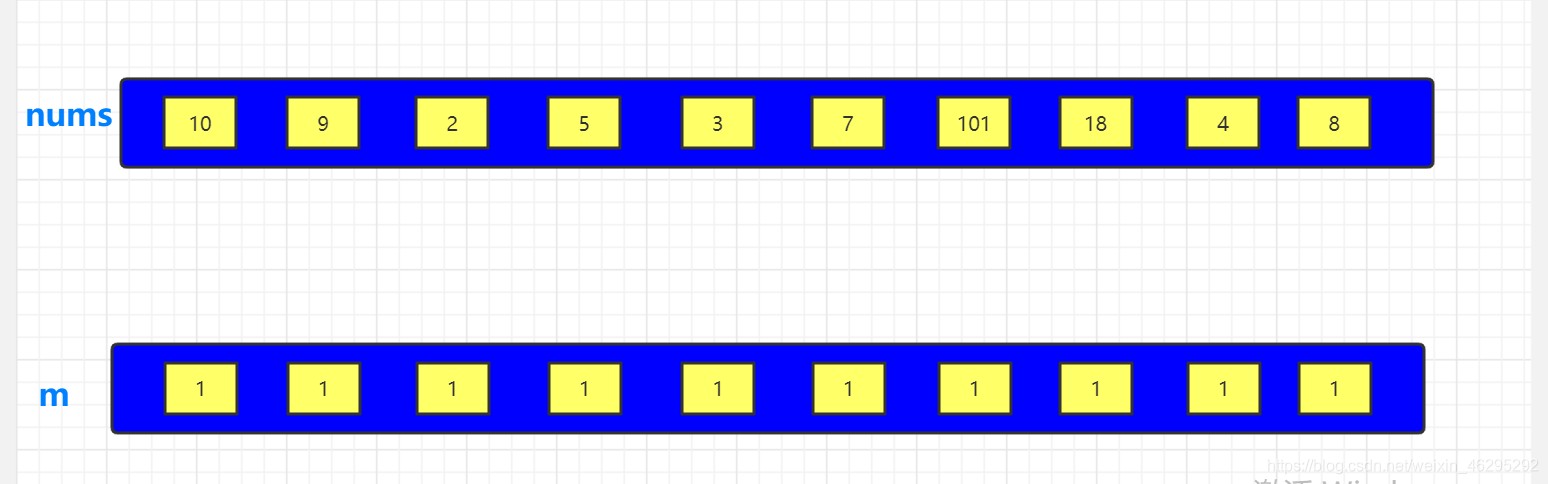
第二步:
依次遍历nums容器的元素,当我遍历第i个元素时,对比前面i-1个元素,如果存在nums[j]

第三步:
返回dp容器中的最大值,即为nums容器的最长上升子序列的长度

class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if(nums.size()==0)
return 0;
vector<int>dp(nums.size(),1);
int maxlen=1;
for(int i=0;i<nums.size();++i)
{
for(int j=0;j<i;j++)
{
if(nums[j]<nums[i])
{
dp[i]=max(dp[j]+1,dp[i]);
if(maxlen<dp[i])
maxlen=dp[i];
}
}
}
return maxlen;
}
};
题解思路:
对于该题解力扣上有十分详细的介绍,有很清晰的PPT演示,这里附上那位大佬的题解链接:题解class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if(nums.size()<2)
return nums.size();
//辅助数组,用来记录最长上升子序列的长度(注意:里面储存的序列,不一定是题意要求的最长上升子序列,但长度一样)
vector<int>m;
m.push_back(nums[0]);
int maxlen=0;//表示辅助数组m的最右边元素的下标,也是该数组值最大的元素下标
for(int i=1;i<nums.size();++i)
{
if(nums[i]>m[maxlen])//如果原数组中元素大于辅助数组末尾值,则辅助数组长度加1
{
m.push_back(nums[i]);
maxlen++;
}
else//使用二分查找找到第一个大于nums[i]的元素,更换它们的数值
{
int left=0,right=maxlen;
while(left<right)
{
int mid=(left+right)>>1;//等价于(left+right)/2,但运行速度要快于后者
if(m[mid]<nums[i])
left=mid+1;
else
right=mid;
}
m[left]=nums[i];
}
}
return maxlen+1;//加一是因为下标和长度偏差1
}
};







