最长上升子序列——线性DP（C++）

AcWing 895. 最长上升子序列
给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数N。

第二行包含N个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围
1≤N≤1000，
−109≤数列中的数≤109
输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

思路

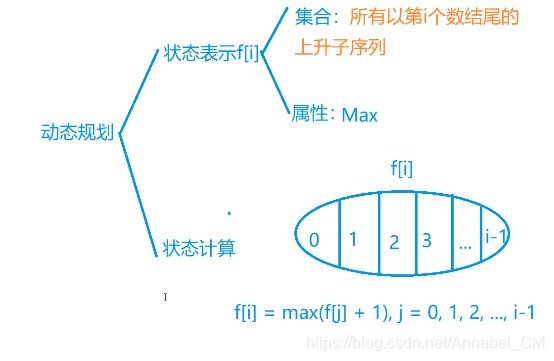
此处要分析动态规划中的状态表示，f[i]的意义是以第i个为结尾的上升子序列，而我们需要求的属性是MAX，对于f[i]我们可以划分为 以i之前一个数为结尾的上升子序列 + 1，此处需满足条件是a[i] > a[j].
最后需要遍历所有f，来存一个最大值

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N], f[N];//f[i]表示所有以i结尾的严格单调上升的子序列的最大长度

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ )
    {
        f[i] = 1; // 只有a[i]一个数,每一个f[i]的初始化都是1，因为最短就是本身，即为1；
        for (int j = 1; j < i; j ++ )
            if (a[j] < a[i])//虽然划分包含所有a[i],但其不一定合法，因此需要提前预判一下
                f[i] = max(f[i], f[j] + 1);
    }

    int res = 0; //通过遍历f数组，来求最大值
    for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);

    printf("%d\n", res);

    return 0;
}

12345678910111213141516171819202122232425262728293031

AcWing 896. 最长上升子序列 II
给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数N。

第二行包含N个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围
1≤N≤100000，
−109≤数列中的数≤109
输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

/*我们遍历原来的a数组，对于每个a[i],我们在q[]数组查找小于a[i]的最大的数x 
找到以后我们将x的后一个数更新成a[i],因为x是小于a[i]的最大的数,那么x的后一个数一定
是大于等于a[i]的.这个也好证明,如果x的后一个数也小于a[i],那么q数组中小于a[i]的的最大的数就不是
x了而是x的后一个数了(数组q单调上升),这与我们二分的结果相反。
*/ 
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int a[N];
int q[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    int len = 0;
    for (int i = 0; i < n; i ++ )// 从短到长解决各个子串的
    {
        int l = 0, r = len;// 二分搜索，得到能接在 a[i] 前面的上升子序列的最大长度 l
        while (l < r)//二分去更新数组q
        {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }

    printf("%d\n", len);

    return 0;
}