背包问题是动态规划算法的经典问题，本节将用背包问题介绍完整的动态规划算法如何解决问题。

1 问题描述

有n件物品，它们有各自的重量和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值，如图所示，装包条件是一种商品只能装一个。

image.png

2 解析问题

由于背包只能装载4kg的东西，所以要想将图7.4中的物品装入包内就需要进行取舍，并且应使得包内的物品价值最高。下面用动态规划算法进行选择。 最简单的方法是尝试使用各种可能的物品组合，找出价值最高的组合，如图所示。

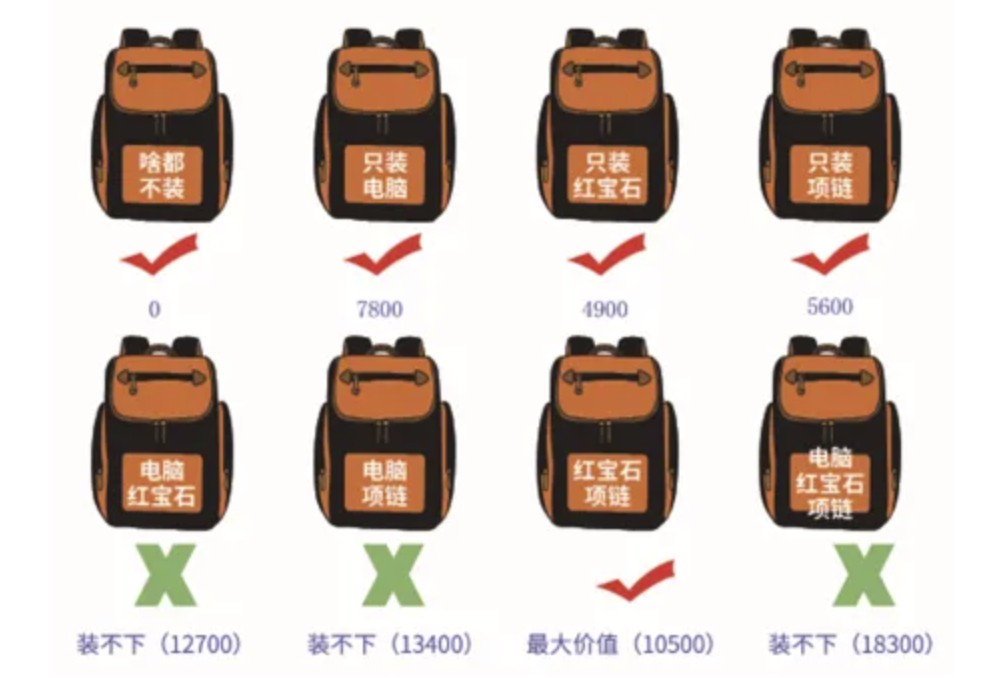
image.png

这种办法是可以的，但是速度非常慢，对于三件物品就需要8次不同组合比较。

如果有四件物品，则需要计算更多的组合。很显然，当物品数量增多时，简单组合方法的速度会变慢，从最优算法角度考虑，这种算法是不可行的。接下来通过动态规划算法快速地找出最优组合。

动态规划算法就是将大问题变成小问题，通过解决小问题逐步解决大问题。因此将大背包变成小背包问题，按照物品的重量分成小背包（即1kg、2kg、3kg、4kg的小背包）。

下面为背包问题创建一个网格，如图所示。

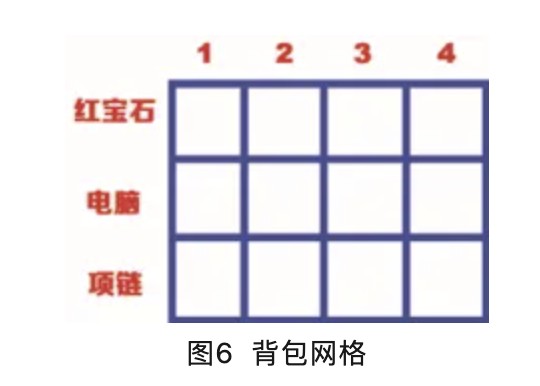
image.png

从图8可以看出，网格的行表示物品（分别为：红宝石、电脑和项链），列表示不同容量的背包（将背包拆分成1kg，2kg，3kg，4kg的小背包），网格最初是空的，通过算法将网格填满，就能够找到答案了。

“红宝石”行

首先计算“红宝石”行的价值，忽略“电脑”行和“项链”行，如图7所示。

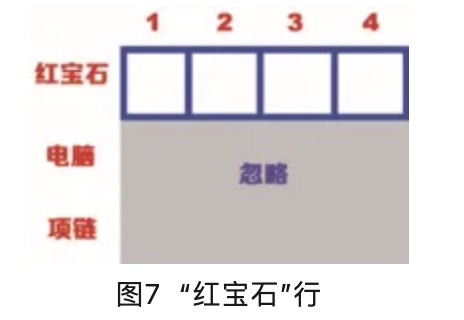
image.png

“红宝石”行的第一个单元格表示背包的容量为1kg，红宝石的重量也是1kg，这说明红宝石能装入背包里，且此时价值为4900，因此填入网格如图8所示。

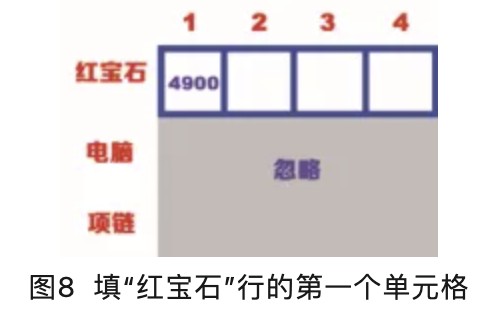
image.png

“红宝石”行的第二个单元格表示背包的容量为2kg，但是此时只有红宝石可以选择，因此第二个单元格的价值是4900，如图9所示。

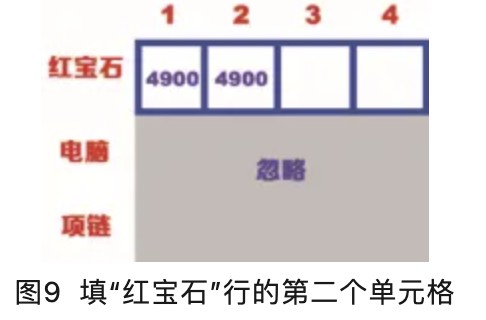
image.png

“红宝石”行的第三个单元格表示背包的容量为3kg，此时也只有红宝石可以选择，因此第三个单元格的价值是4900，如图10所示。

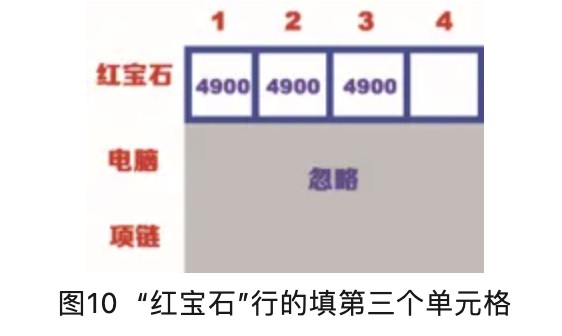
image.png

“红宝石”行的第四个单元格表示背包的容量为4kg，此时也只有红宝石可以选择，因此第四个单元格的价值是4900，如图11所示。

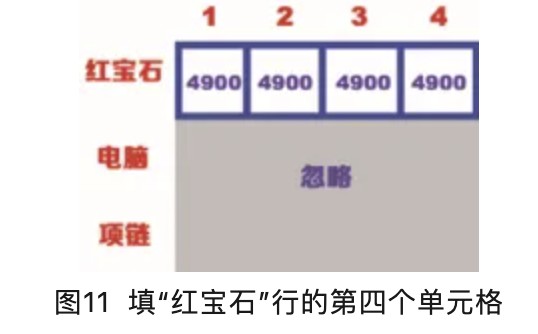
image.png

此时，“红宝石”行表格被填满，且最大价值是4900，就表示如果在容量为4kg的背包中只装红宝石，那么可装入的最大价值是4900。

“电脑”行

计算“电脑”行的价值，这里忽略“项链”行，如图12所示。

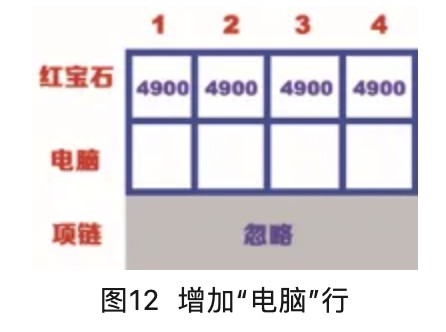
image.png

“电脑”行的第一个单元格表示背包的容量为1kg，而电脑的重量是4kg，因此背包此时装不下电脑。但是当背包为1kg时可以放入价值为4900的红宝石，因此“电脑”行的第一个单元格的价值也是4900，如图13所示。

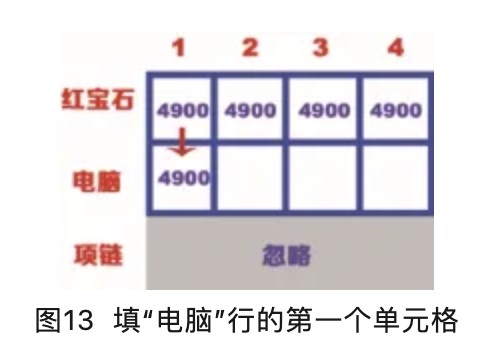
image.png

“电脑”行的第二个单元格表示背包的容量为2kg，而电脑的重量是4kg，因此背包此时也装不下电脑。但是当背包容量为2kg时，可以放入价值为4900的红宝石，因此“电脑”行的第二个单元格的价值也是4900，如图14所示。

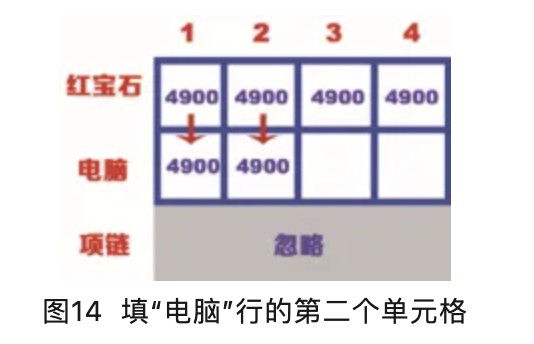
image.png

“电脑”行的第三个单元格表示背包的容量为3kg，而电脑的重量是4kg，因此背包此时也装不了电脑。但是当背包为3kg时，可以放入价值为4900的红宝石，因此“电脑”行的第三个单元格的价值也是4900，如图15所示。

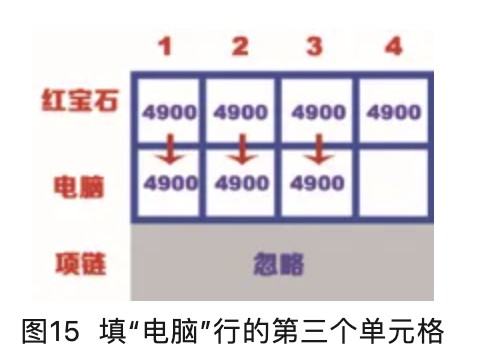
image.png

“电脑”行的第四个单元格表示背包的容量为4kg，电脑的重量是4kg，此时背包中能装入电脑，第四个单元格的价值为7800，如图16所示。

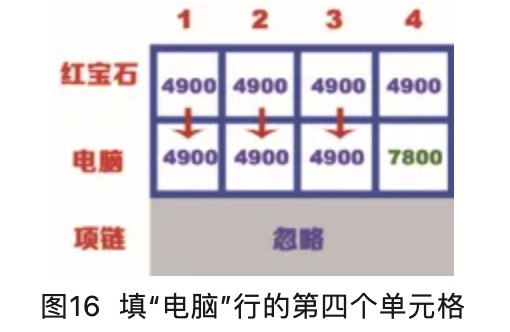
image.png

到这里，“电脑”行表格也被填满了，且最大值是7800，就表示在容量4kg的背包装电脑时，价值最大。

“项链”行

计算“项链”行的价值，如图17所示。

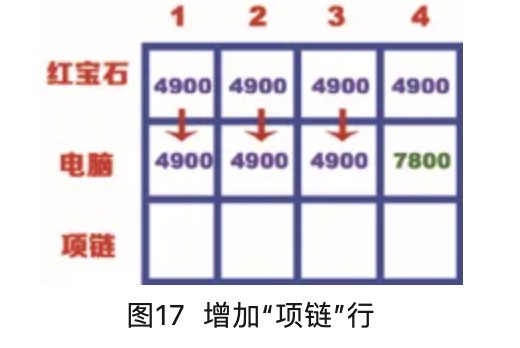
image.png

“项链”行的第一个单元格表示背包的容量为1kg，而项链的重量是3kg，因此背包此时装不下项链。当背包为1kg时，可以放入价值为4900的红宝石，因此“项链”行的第一个单元格的价值也是4900，如图18所示。

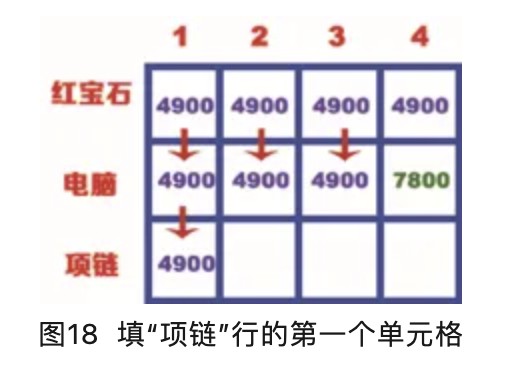
image.png

“项链”行的第二个单元格表示背包的容量为2kg，而项链的重量是3kg，因此背包此时装不下项链。当背包为2kg时，可以放入价值为4900的红宝石，因此“项链”行的第二个单元格的价值也是4900，如图19所示。

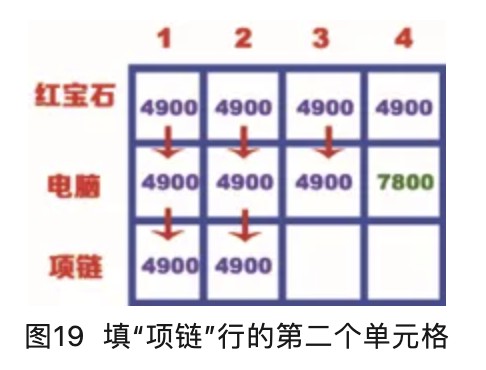
image.png

“项链”行的第三个单元格表示背包的容量为3kg，此时背包可以装下项链，项链的价值是5600。也可以放入价值是4900红宝石。很明显，5600比4900大，因此背包容量为3kg时，最大价值为5600，如图20所示。

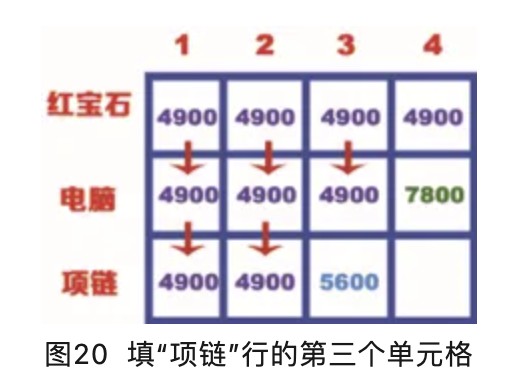
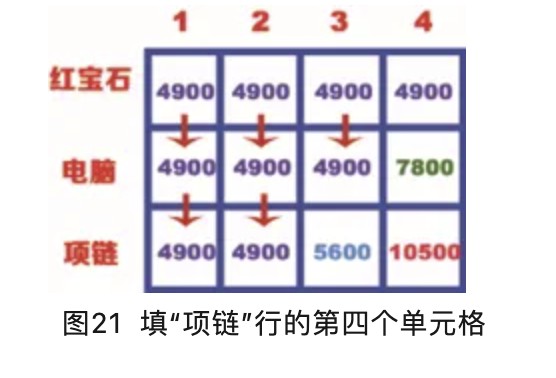
image.png

“项链”行的第四个单元格表示背包的容量为4kg，项链的重量为3kg，此时背包可以装下项链，也可以装下红宝石，也可以装下电脑。从网格来看，背包容量是4kg的时候，目前最大的价值是7800，而项链的价值是5600，所以只装项链，不装电脑，很显然不合适。 但是项链的重量只有3kg，背包剩余1kg的容量，上文讲到，1kg的重量最大价值是4900，这就表明还可以装入红宝石，此时背包同时装入项链和红宝石。 其价值最大为10500，如图21所示。

image.png

总结

由图21可知，在背包中装入项链和红宝石得到的价值最大，即10500。 图7~图21计算单元格的价值时使用的公式都是相同的，公式如下：

image.png

通过公式计算出每个单元格的价值，并最终得到最大价值的过程就是将大问题拆成小问题，最后再合并大问题，从而得出了大问题的解。而这个解题的过程就是动态规划算法，如图23所示。

image.png

3 代码实现

实例1 “背包问题”
接下来用Python代码来实现“背包问题”，具体代码如下：

"""
功能：自定义背包函数，实现动态规划算法
参数说明：count：表示物品件数
          TotalWeight:表示背包的总容量
          weight：表示每件物品的重量
          cost：表示每件物品的价值
"""
def bag(count, TotalWeight, weight, cost):
# 置零，表示初始状态
value = [[0 for j in range(TotalWeight + 1)] for i in range(count +1)]
    for i in range(1, count+1):                     # 遍历物品件数，从第1件物品计算
        for j in range(1, TotalWeight + 1):            # 遍历背包容纳量，从重量为1开始计算
            value[i][j] = value[i - 1][j]              # 定义value数组存储最大价值
            # 背包总容量够放当前物体，遍历前一个状态考虑是否置换
            if j >= weight[i - 1] and value[i][j] < value[i - 1][j - weight[i - 1]] + cost[i - 1]:
                # 最大价值：当前物品的价值+剩余空间的价值
                value[i][j] = value[i - 1][j - weight[i - 1]] +cost[i - 1]
    for x in value:                             # 遍历输出背包网格
        print(x)
    return value                              # 返回最大价值
"""
功能：自定义显示输出结果函数
参数说明：count：表示物品件数
          TotalWeight:表示背包的总容量
          weight：表示每件物品的重量
          value：表示最大价值，即所求的结果
"""
def show(count, TotalWeight, weight, value):
    x = [False for i in range(count)]                  # 初始化x，使得x为假
    j = TotalWeight                          # 背包的容量赋给变量j
    for i in range(count, 0, -1):                     # 遍历每个物品
        # 如果value[i][j]单元格大于上一行同列的单元格的价值，进行更新
        if value[i][j] > value[i - 1][j]:               
            x[i - 1] = True
            j -= weight[i - 1]                  # 总容量减去上一行同列的单元格的重量
    print('最大价值为:', value[count][TotalWeight]) # 输出最大价值的值
    print('背包中所装物品为:')
    for i in range(count):                                   # 遍历物品数
        if x[i]:                                    # 判断最大价值的物品数
            print('第', i + 1, '个 ', end='')        # 输出是第几个物品
 
count = 3                                   # 一共有3件物品
TotalWeight = 4                             # 背包的总容量是4
weight = [1, 4, 3]                             # 每个物品的重量
cost = [4900, 7800, 5600]                       # 每个物品的价值
value = bag(count, TotalWeight, weight, cost)          # 调用bag()函数动态规划算法函数
show(count, TotalWeight, weight, value)            # 调用show()函数输出结果

程序运行结果如图24所示。

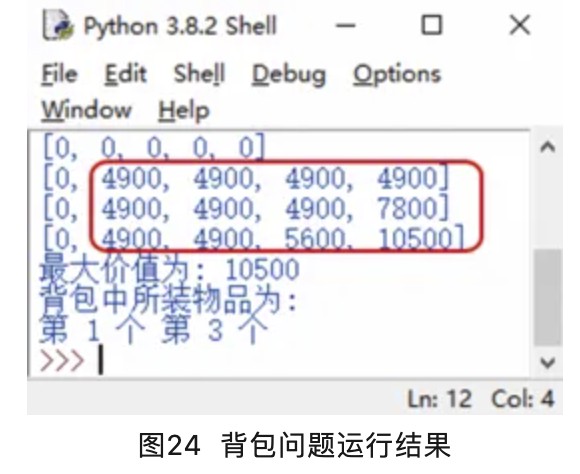
image.png

从运行结果得知，红框中的数据和图24所示的背包网格数据吻合，最后输出的物品是第1个和第3个，即红宝石和项链，完全吻合2小节的讲解结果。

文章来源：明日科技 公众号：明日IT部落