说明
树老师爬楼梯,他可以每次走1级或者2级,输入楼梯的级数,求不同的走法数。 例如:楼梯一共有3级,他可以每次都走一级,或者第一次走一级,第二次走两级,也可以第一次走两级,第二次走一级,一共3种方法。
输入格式
输入包含若干行,每行包含一个正整数N,代表楼梯级数,1≤N≤30。
输出格式
不同的走法数,每一行输入对应一行输出。
问题分析
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?是引用
当n=1时,只需爬一个台阶,就是一种解法。
当n=2时,可以走两次一层或者走一次2层。
当n=3时,此时你可能在第一层或者第二层,当在第一层时相当于你在第0层准备去往第二层,当在第二层时相当于你在第0层准备去往第1层。
以此类推。
1.递归调用
int climbStairs(int n)
{
if(n==1||n==2){
return n;
}else{
return climbStairs(n-1)+climbStairs(n-2);
}
}
时间复杂度:(2^n)
空间复杂度:(n)
运用了递归耗时较久。
2.优化递归调用
在方法一的递归中,实际上在递归遍历的过程中经过了许多重复的结点,因此我们可以利用一个数组存储已经遍历过的结点,降低时间复杂度。
int climStairsMemo(int n,int *memo){
if(memo[n]>0){
return memo[n];
}
if(n==1||n==2){
memo[n]=n;
}else{
memo[n]=climStairsMemo(n-1,memo)+climStairsMemo(n-2,memo);
}
return memo[n];
}
int climbStairs(int n)
{
int* memo=(int*)malloc((n+1)*sizeof(int));
for(int i=0;i<n+1;i++){
memo[i]=0;
}
return climStairsMemo(n,memo);
}
时间复杂度:(N)
空间复杂度:(N)
3.动态规划
int climbStairs(int n)
{
if(n==1){
return 1;
}
int dp[n+1];
for(int i=0;i<n+1;i++){
dp[i]=0;
}
dp[1]=1;
dp[2]=2;
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
实际上是递归方法的非递归实现。
时间复杂度:(N)
空间复杂度:(N)
4.滚动数组(优化方法3)
实际上在方法三调用的过程中,仅有两个值是需要选取的,即在我们题目分析时候提到的前一层和前两层台阶的值。
int climbStairs(int n)
{
if(n==1){
return 1;
}
int first=1;
int second=2;
int third;
for(int i=3;i<=n;i++){
third=second+first;
first=second;
second=third;
}
return second;
}
时间复杂度:(N)
空间复杂度:(1)
斐波那契数列通项公式
在前几种方法中就可以看到这个题目其实运用到了斐波那契数列的思想,因此我们可以直接通过斐波那契数列通项公式进行求解
将通项公式:
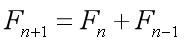
转化为矩阵形式:
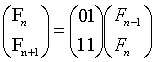
设M为矩阵
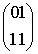
通过转化可以得到表达式,
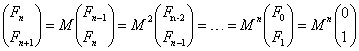
然后再展开
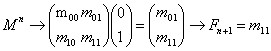
现在就可以得知,这个矩阵右下角的取值即我们需要求的
public class Solution{
public int[][] multiply(int [][]a,int [][]b){
int[][] c=new int[2][2];
c[0][0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
c[0][1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
c[1][0]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
c[1][1]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
return c;
}
int int[][] pow(int[][]a,int n){
int[][] ret ={{1,0},{0,1}};
while(n>0){
if((n&1)==1){
ret=multiply(ret,a);
}
n>>=1;
a=multiply(a,a);
}
return ret;
}
int climbStairs(int n)
{
int[][] m={{0,1},{1,1}};
int[][] res=pow(m,n);
return res[1][1];
}
}
时间复杂度:(log(n))
空间复杂度:(1)
6.运用斐波那契数列直接计算
对方法五中的矩阵M进行对角化
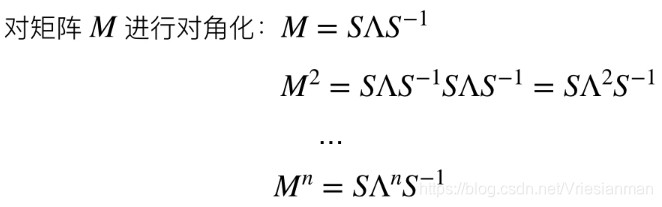
然后求出特征值和特征向量为:
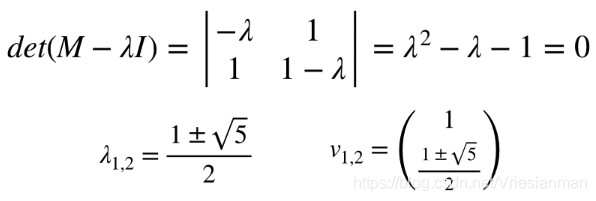
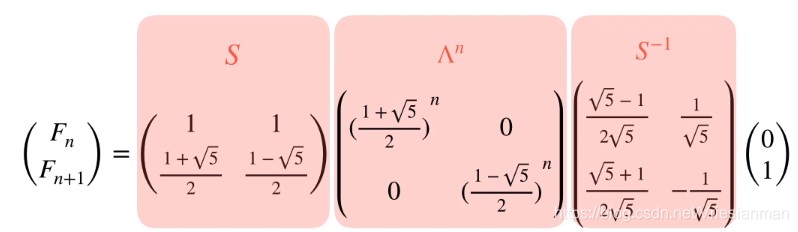
然后就可以直接计算出
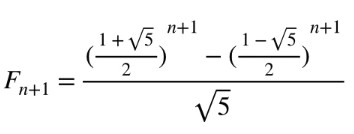
因此这时的代码就很简洁:
int climbStairs(int n)
{
double sqrt5=sqrt(5);
double result=(pow((1+sqrt5)/2,n+1)-pow((1-sqrt5)/2,n+1))/sqrt5;
return (int)result;
}
这就是斐波那契数列求爬楼梯的一些方法总结.
希望我的学习笔记可以帮助到大家,感谢!







