百钱百鸡问题的多种解法

2023年 gesp 考级中有https://ok.hn.cn/p/GESP2303C2A 关于百钱买百鸡的试题：

从百钱百鸡问题说起

关于枚举，我们从一个经典的百钱百鸡问题说起：

题目：我国古代数学家张丘建在《算经》一书中曾提出过著名的“百钱买百鸡”问题，该问题叙述如下：鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一；百钱买百鸡，则翁、母、雏各几何？翻译过来，意思是公鸡一个五块钱，母鸡一个三块钱，小鸡三个一块钱，现在要用一百块钱买一百只鸡，问公鸡、母鸡、小鸡各多少只？

直接枚举（暴力破解）

对于此题，我们有一种无脑思路，就是将每一种买鸡的情况罗列出来，由计算机来检查是否符合题目的要求，我们很容易通过程序来解决这个问题，如下：

#include <stdio.h>
int main() {
    int x, y, z; // x为公鸡，y为母鸡，z为小鸡
    for (x = 0; x < 100; x++)
        for (y = 0; y < 100; y++)
            for (z = 0; z < 100; z += 3) {
                if (x + y + z == 100 && 5 * x + 3 * y + z / 3 == 100) {
                    printf("公鸡：%d只  母鸡：%d只  小鸡：%d只\n", x, y, z);
                }
            }

    return 0;
}

输出结果：

很简单，我们便得到了答案。这时可能就有同学要说了：“就这？这么简单，还用你来说吗？”但是，枚举之所以能称为算法，自然不会这么简单！

开始优化（缩小枚举范围）

对于枚举，我们可以进行优化，而不是单单像上面那样无脑列出每一个结果，那么该如何优化呢？这就需要我们从题目中获取信息了。首先我们想，是否可以缩小枚举数据的范围，从而减少枚举的情况个数。对于本题，我们不难发现，公鸡和母鸡的数目不用从0枚举到100，买到的公鸡在达到20只时，就已经达到了预期的100元。同理，母鸡不能超过33只，据此，我们可以修改程序，将循环的范围缩小。同时，在程序中加入clock（）函数，以此检查程序运行的速度是否变快。为了减小误差带来的影响，我们不妨将题目改为万钱万鸡问题（笔者以此刻意地增加运行时间，以此减小误差对实验结果的影响）。代码如下：

#include <stdio.h>
#include <time.h>
int main() {
    int x, y, z; // x为公鸡，y为母鸡，z为小鸡
    for (x = 0; x < 2000; x++)
        for (y = 0; y < 3333; y++)
            for (z = 0; z < 10000; z += 3) {
                if (x + y + z == 10000 && 5 * x + 3 * y + z / 3 == 10000) {
                    printf("公鸡：%d只  母鸡：%d只  小鸡：%d只\n", x, y, z);
                }
            }

    printf("The time was:%.5lfs", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

运行结果

我们再来对比优化前的结果

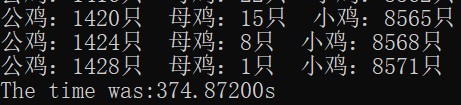
OK，我们明显可以发现，优化前后两者运行时间的区别，看来枚举也不是完全无脑的！

继续优化（二重循环）

我们来进一步思考，仅仅是缩小了循环的终止条件，运行时间就差距如此之大，我们不妨想办法直接去掉一重循环，那么运行时间必然可以更快！

我们不妨这样想，我们先确定公鸡和母鸡的个数，然后剩下的钱全部用来买小鸡，我们只需要判断能不能正好花完10000元，以及是否正好买到10000只鸡即可，于是我们将判断条件改为

if((5*x+3*y+(10000-x-y)/3.0)==10000)

如果5*x+3*y+(10000-x-y)/3.0的值不是整数，则表示不能正好花完10000元；在该式值为整数的情况下，我们判断其值是否为10000，为真则表示买到了10000只鸡，符合题目要求。完整代码如下：

#include <stdio.h>
#include <time.h>
int main() {
    int x, y; // x为公鸡，y为母鸡，z为小鸡
    for (x = 0; x < 2000; x++)
        for (y = 0; y < 3333; y++) {
            if ((5 * x + 3 * y + (10000 - x - y) / 3.0) == 10000) {
                printf("公鸡：%d只  母鸡：%d只  小鸡：%d只\n", x, y, (10000 - x - y) / 3);
            }
        }

    printf("The time was:%.5lfs", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

运行结果：

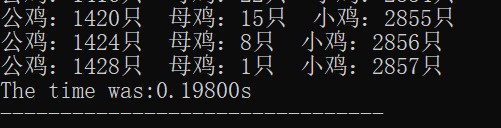
我们惊讶地发现，运行时间居然直接缩小了两个量级！

最终优化（一重循环）

在尝到直接削去一重循环带来的甜头后，不知足的我们又开始想，是否可以再削去一重循环，只用一重循环来解决呢？我们反观上面的二重循环，发现我们并没有使用z这个变量了，那么我们在只使用一重循环的时候，是否也应该只使用一个变量呢？我们想到，x,y,z之间并不是毫无联系的，我们假设万钱刚好买到万鸡，据此我们列出两个方程组：

5*x+3*y+z/3=10000

x+y+z=10000

我们进行数学消元，只保留x，得到y=2500-7*x/4和z=7500+3*x/4，这是我们假设条件成立得到的关系式，下面我们只需令x取不同的值，同时对y和z进行检查，若x,y,z均满足我们预设的条件，那么这组解就是有效的。对于y，我们要令其为非负数，所以x不能大于1428；对于z，我们要令其为3的倍数。此外，我们得到的y和z两个关于x的关系式是由假设上述两个方程组成立得到的，所以我们的解还需要满足上述两个关系式。据此，我们得到以下的代码：

#include <stdio.h>
int main() {
    int x, y, z; // x为公鸡，y为母鸡，z为小鸡
    for (x = 0; x < 1429; x++) {
        y = 2500 - 7 * x / 4;
        z = 7500 + 3 * x / 4;
        if ((x + y + z == 10000) && (5 * x + 3 * y + z / 3 == 10000) && (z % 3 == 0))
            printf("公鸡：%d只  母鸡：%d只  小鸡：%d只\n", x, y, (10000 - x - y) / 3);
    }
    return 0;
}

这时由于其运行时间已经很小，我们再比较运行时间受误差的影响很大，不能再比较运行时间。但是我们可以通过比较循环次数来对比两种算法，在二重循环，我们的循环次数是2000*3333=6666000次，而在一重循环中，我们的循环次数仅仅是1429次，缩小了三个量级，那么运行速度理所应当地更快了。