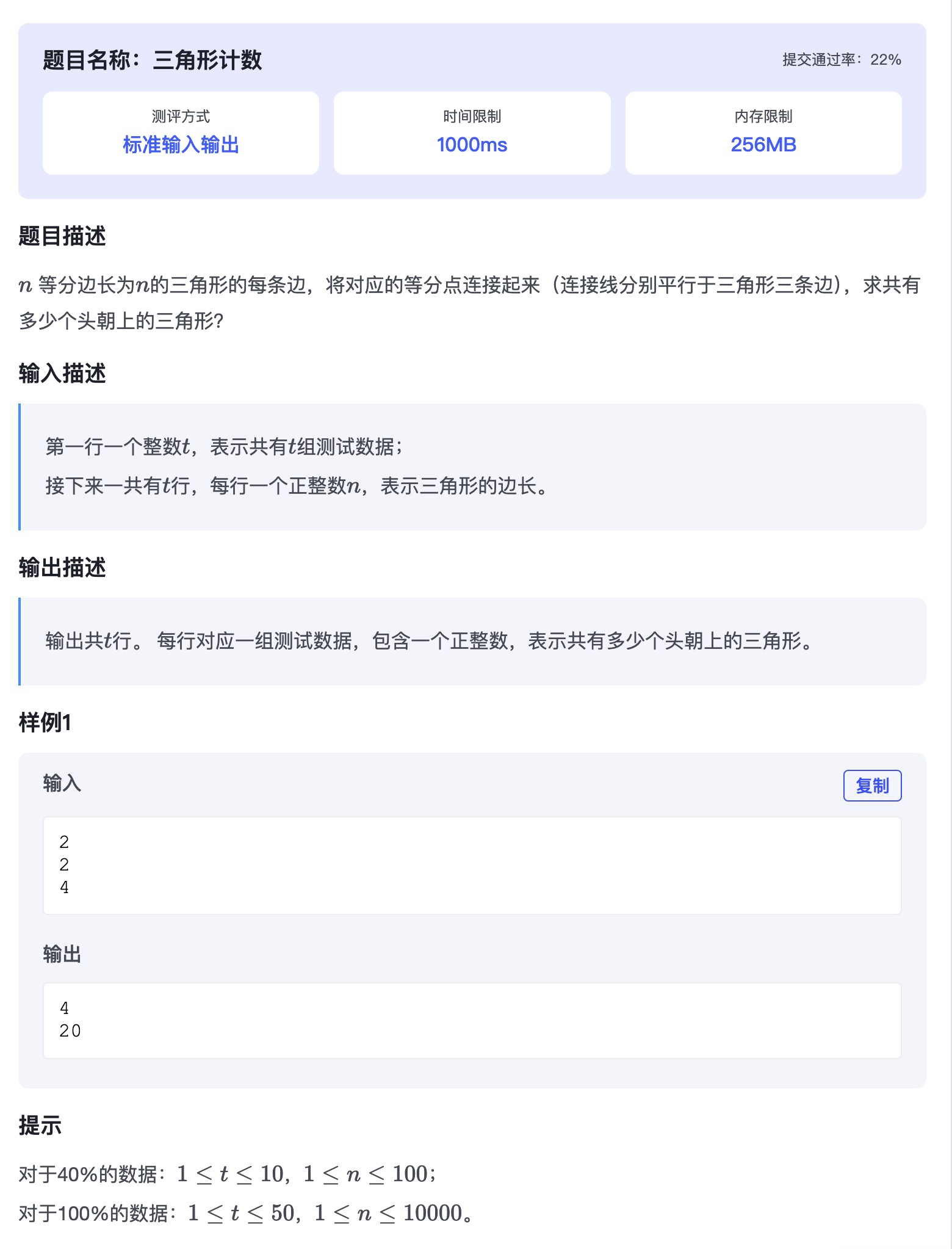
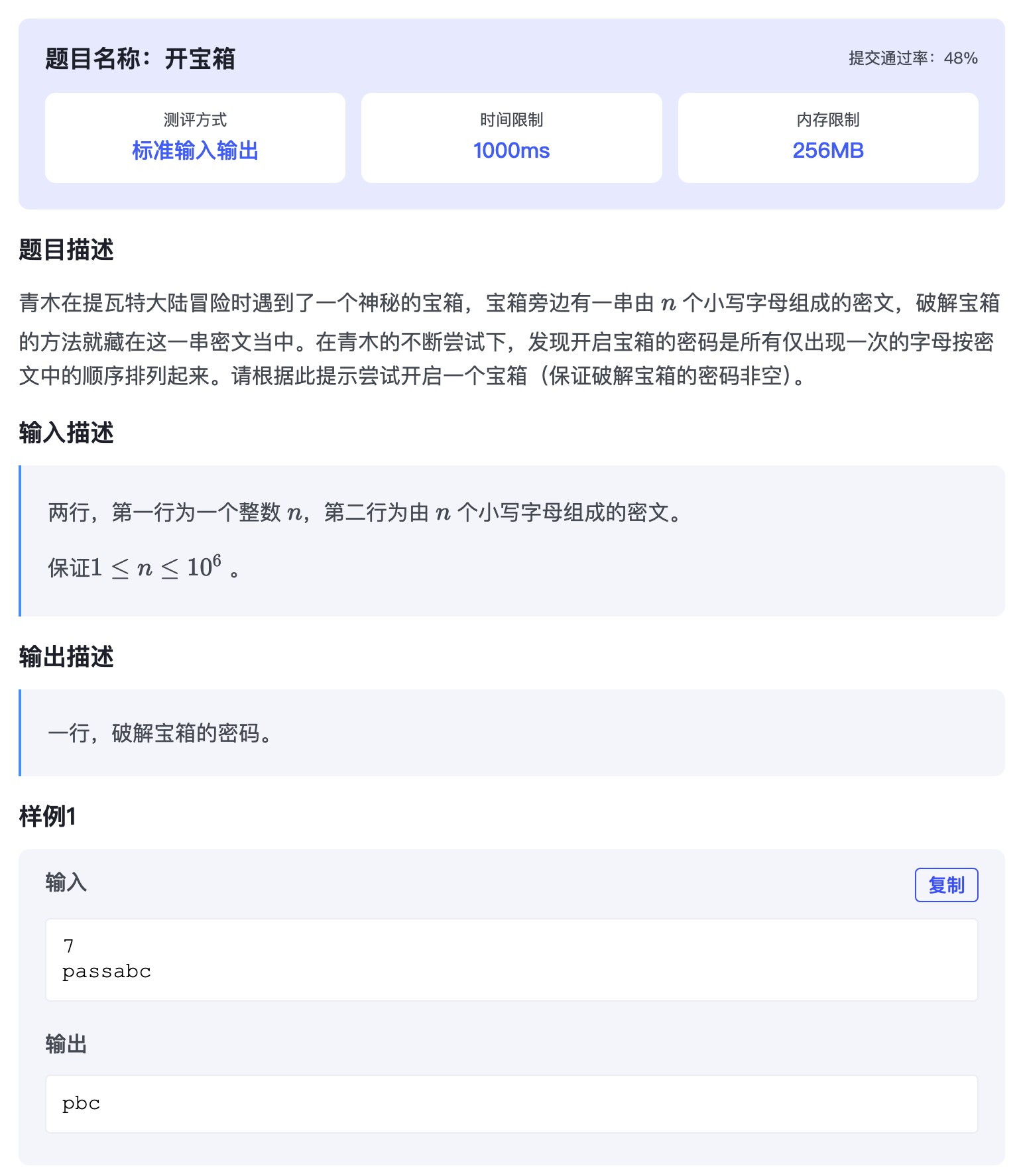
题目来源：https://ok.hn.cn/p/1532

描述

把m个同样的苹果放在n个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？

注意：如果有7个苹果和3个盘子，（5，1，1）和（1，5，1）被视为是同一种分法。

数据范围：0 <= m <= 10 ，1 <= n <= 10 。

输入描述：

输入两个int整数

输出描述：

输出结果，int型

示例1

输入：

7 3

输出：

8

分析

方法1递归

目标函数：f(m, n) ——> m个苹果放入n个盘子的放法

case 1:f(m, n) = f(m,m) , m < n

m < n——>盘子数大于苹果数，此时我们发现盘子数再多也无济于事，他的放法最多为f(m,m).

比如 2个苹果 2个盘子有两种：{0, 2} {1, 1} 再加一个盘子 {0, 2, 0} {1, 1, 0} 空盘无意义

case 2:m>n

苹果数大于盘子数，这是游客分为两种情况

a’:存在空盘情况,也就是至少有一个空的盘子，那么问题转化为 m个苹果放入n-1个盘子里的问题

f(m, n)=f(m,n-1)

b’:没有空盘，也就是每个盘子至少放一个苹果，那么问题转化为m-n个苹果放入n个盘子里的问题

f(m, n)=f(m-n,n)

代码

def solve(m, n):
    if m == 1 or m == 0 or n == 1 or n == 0:
        return 1
    if m < n:
        return solve(m, m)
    else:
        return solve(m-n, n) + solve(m, n-1)



m, n = map(int, input().split())  # m 苹果 n 盘子
print(solve(m, n))

方法2动态规划：

动态规划的主要目标就是找寻状态转移方程

通过方法1的分析我们可以得到状态转移方程：

[1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 2, 2, 3, 3, 4, 4]
[1, 1, 2, 3, 4, 5, 7, 8]

初始化前两行 前两列都为1，

因为1或0个盘子放再多的苹果也只有1种方法

因为1或0个苹果用再多的盘子也只有1种方法

m, n = map(int, input().split())  # m 苹果 n 盘子
dp = [[0]*(m+1) for i in range(n+1)]
for i in range(m+1):
    dp[0][i] = dp[1][i] = 1
for i in range(2,n+1):
    dp[i][0] = dp[i][1] = 1
for i in range(2, n+1):
    for j in range(2, m+1):
        dp[i][j] = dp[j][j] if i > j else dp[i-1][j] + dp[i][j-i]
print(dp[n][m])