第5关 - 2019NH教师GoC组测试题
693.1. 小丑的帽子(2019NH教师GoC)
题目描述
如下图，三角形边长100，球的半径20。请编程画出这个图形。
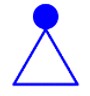
题解
int main(){
p.oo(20);
p.bk(20)
.rt(150).fd(100)
.rt(120).fd(100)
.rt(120).fd(100);
return 0;
}
694.2. 四周花边(2019NH教师GoC)
题目描述
如下图，四边的颜色号为0、1、2、3，每个小段的线段长度是20。请编程画出这个图形。
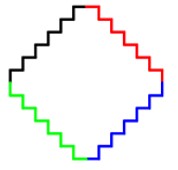
题解
为了方便大家理解梯形路线的重复规律，这里不使用二重循环，大家可以自行优化。
int main(){
for(int i = 0; i<4; i++){
p.c(i)
.fd(20).rt(90)
.fd(20).lt(90)
.fd(20).rt(90)
.fd(20).lt(90)
.fd(20).rt(90)
.fd(20).lt(90)
.fd(20).rt(90)
.fd(20).lt(90)
.fd(20).rt(90)
.fd(20).lt(90)
.fd(20).rt(90)
.fd(20).lt(90)
.rt(90);
}
return 0;
}
695.3. 外半径与内半径(2019NH教师GoC)
题目描述
有n个不同的正整数，如果使用他们作为半径画圆，会有n个圆。例如：n=5时，有5个不同正整数:100 20 120 80 160，图形如下：
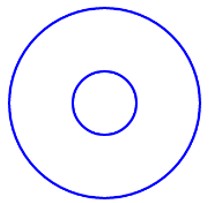
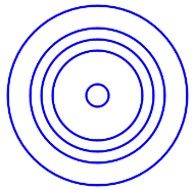现在希望只是画最外的圆和最里的圆，比如上面的图就变为：
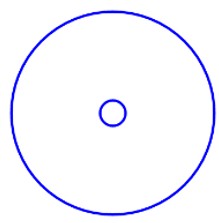
输入格式
第一行1个整数n；（2<=n<=20）第二行n个不同的正整数（不超过300），空格隔开。
输出格式
正确的图形。
输入/输出例子1
输入：
4
112 150 50 90
输出：
696.4. 相同数(2019NH教师GoC)
题目描述
小G和小C是好朋友，他们正一起并肩登走路。走路很无聊，他们想了一个游戏，小G边走边报数：1 2 3 1 2 3 1 2 3 …. ；小C边走边报数： 1 2 1 2 1 2 1 2 …. 。如果某一步他们报的数相同，就会觉得很碰巧。
在一条红色（1号颜色）直线上，每隔25画一个为半径10的圆或边长20的正方形表示脚印：如果某一步小G和小C报的数相同就用圆表示，否则就用正方形表示。
输入格式
一行1个正整数n，表示他们走的步数。n<=15输出格式
正确的图形
输入/输出例子1
输入：
10
输出：
题解
本题重点是解决循环中最后一次循环，fd(25) 多绘制一次的问题。
方法一：
int main(){
int n;
cin >> n;
int l = 25 * (n-1);
p.rt(90).c(1)
.fd(l).bk(l)
.up();
for(int i = 0; i<n;i++){
if(i%3 == i%2){
p.oo(10);
}else{
p.rr(20,20);
}
p.fd(25);
}
return 0;
}
方法二：
int main(){
int n;
cin >> n;
p.rt(90).c(1);
for(int i = 0; i<n;i++){
if(i%3 == i%2){
p.oo(10);
}else{
p.rr(20,20);
}
if(i<n-1){
p.fd(25);
}
}
return 0;
}
方法三：
int main(){
int n;
cin >> n;
p.rt(90).c(1);
for(int i = 0; i<n;i++){
if(i == (n-1)){
p.up();
}
if(i%3 == i%2){
p.oo(10);
}else{
p.rr(20,20);
}
p.fd(25);
}
return 0;
}
697.5. 倒背如流(2019NH教师GoC)
题目描述
黑板上老师写了n给不同的整数（都不包含数字0），小C想考考大家的“倒背如流”能力，从右向左读数字。按照这个次序，用这些颠倒的数为高，从左到右间隔20画n条垂直的线。用绿色（3号颜色）画。
输入格式
第一行1个整数n；（2<=n<=20）第二行n个不同的正整数，空格隔开。
输出格式
正确的图形。
输入/输出例子1
输入：
4
112 231 251 19
输出：
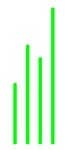
样例解释
先画长度是91的线，后面依次是152、132、211的。
本题用到了数字翻转功能，使用求余取商的方法再重新拼接数字。
数列反转使用 反向绘图的小技巧，原数列可以看成从左向右的方向，而翻转后可以看成从右向左方向
题解
int main(){
cinWin();
p.c(3);
int n ;
cin >> n;
for(int i = 0;i < n ; i++){
int newNum = 0,tmp,num;
cin >> tmp;
// 求翻转数
while(tmp){
num = tmp % 10;
tmp = tmp / 10;
newNum = newNum*10 + num;
}
cout << newNum << " ";
// 反向输出，即从右往左画线
p.moveTo(-20*i,0).fd(newNum).bk(newNum);
}
return 0;
}
698.6. 盘绕(2019NH教师GoC)
题目描述
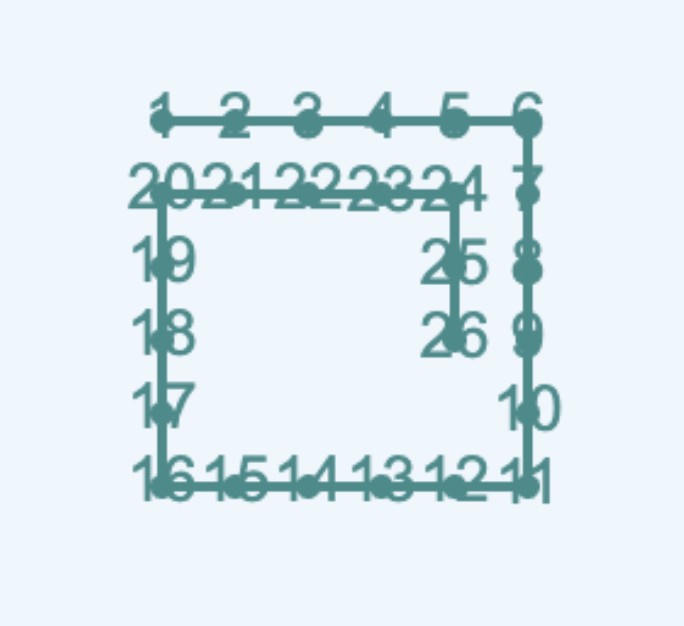
在一个n*n的方格（边长30）迷宫上，通道从左上角开始，顺时针环绕，逐步向里面盘绕。下面用数字标识了一个6*6的迷宫环绕次序。
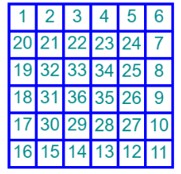
现在，小G按照这个环绕次序走了m步，把到达的每一个方格的中点用12号颜色半径为5的实心圆表示，并依次用线连接起来，就成为一个盘绕的线。请编程画出这个盘绕的线。
输入格式
第一行2个正整数n、m。n<=10， m<=n*n。输出格式
正确的图形。
输入/输出例子1
输入：
4 16
输出：
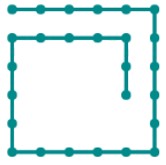
输入/输出例子2
输入：
6 26
输出：
题解（待优化）
int main(){
cinWin();
int n,a,b,m;
cin >> n >> m;
a=1;
b= 30;
p.rt(90).c(12);
for(int i = 0; i< n; i++){
int len = n-1 - i*2;
if(len==0){
//p.oo(5).hide();
return 0;
}
for(int k=0;k<4;k++){
for(int j=0;j<len;j++){
p.oo(5);
if(a<m && j < len -1){
p.fd(b);
}
a++;
if(a > m ){
p.hide();
return 0;
}
}
if(k < 3){
p.fd(b).rt(90);
}
else{
p.rt(90).fd(b);
}
}
}
}
方法二：
回形矩阵 n，最大数量为n*n 所以，大循环使用n 来控制，每次走一个 L 形阶梯，进行顺时针环绕，就可以依次完成。
再使用特判断，第一个 fd(30) 抬笔不画线。
int main() {
cinWin();
int n, m;
cin >> n >> m;
int len = n;
int cnt = 0;
p.rt(90).c(12).hide().up();
for (int j = 0; j < n; j++) {
// 先画一个 L 形 阶梯，
len = n - j;
for(int i = 0; i < len; i++){
cnt ++;
if(cnt > 1) p.down();
if(cnt > m) return 0;
p.fd(30).oo(5);
}
p.rt(90);
for(int i = 0; i < len-1; i++){
cnt ++;
if(cnt > m) return 0;
p.fd(30).oo(5);
}
p.rt(90);
}
return 0;
}
