信奥赛C++编程所需基础数学知识

<cmath>数学库中的函数

image.png

#include <iostream>  
#include <cmath>
using namespace std; 

int main(){
	
	// 向上取整
    cout << ceil(3.5) << " " << ceil(-3.5) << endl;
    
    // 向下取整
    cout << floor(3.5) << " " << floor(-3.5) << endl;
    
    // int 取整
    cout << int(3.5) << " " << int(-3.5) << endl;
    
    // 开方
    cout << sqrt(2) << " " << sqrt(9) << endl;
    
    // 乘方\幂
    cout << pow(2, 10) << endl;
    
    // 四舍五入
    cout << round(3.5) << " " << round(3.49) << endl;
    cout << int(3.5 + 0.5) << endl;
    
    // log 对数  底默认为自然数 e = 2.71828..... 无限不循环
    cout << log(2.71828) << endl;
    cout << log(10) / log(2) << endl;
    
	return 0;
}

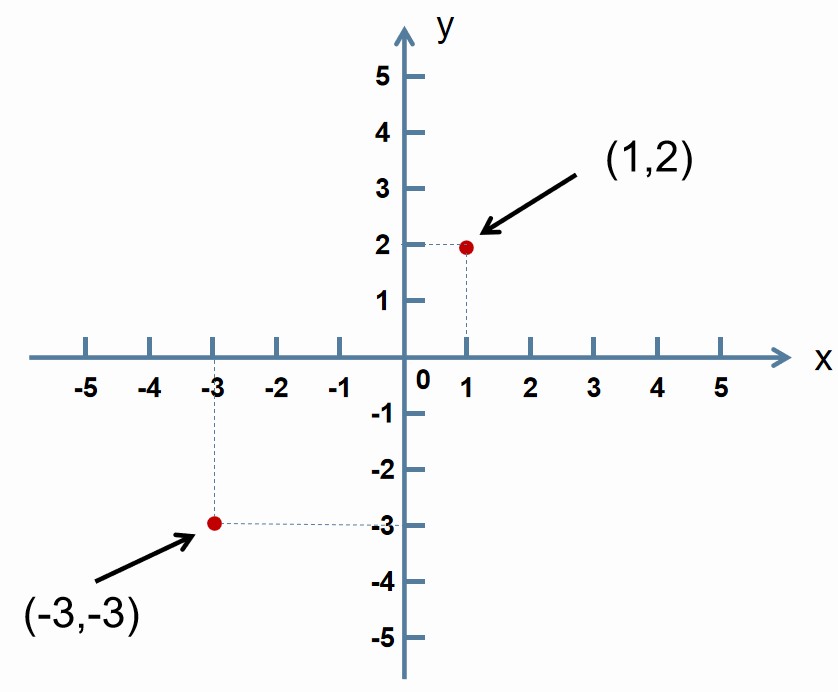
平面直角坐标系

在平面内画两条互相垂直，并且有公共原点的数轴。 其中横轴为X轴，纵轴为Y轴。 这样我们就说在平面上建立了平面直角坐标系。

坐标系中表示点的坐标 (x坐标, y坐标)

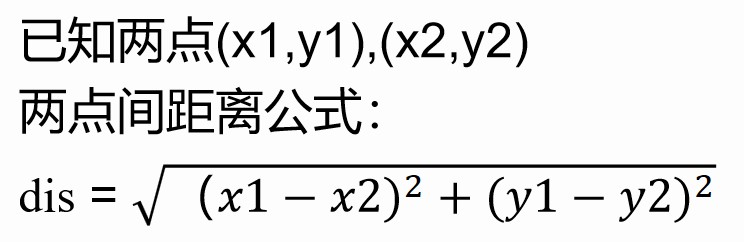
image.png

两点距离公式

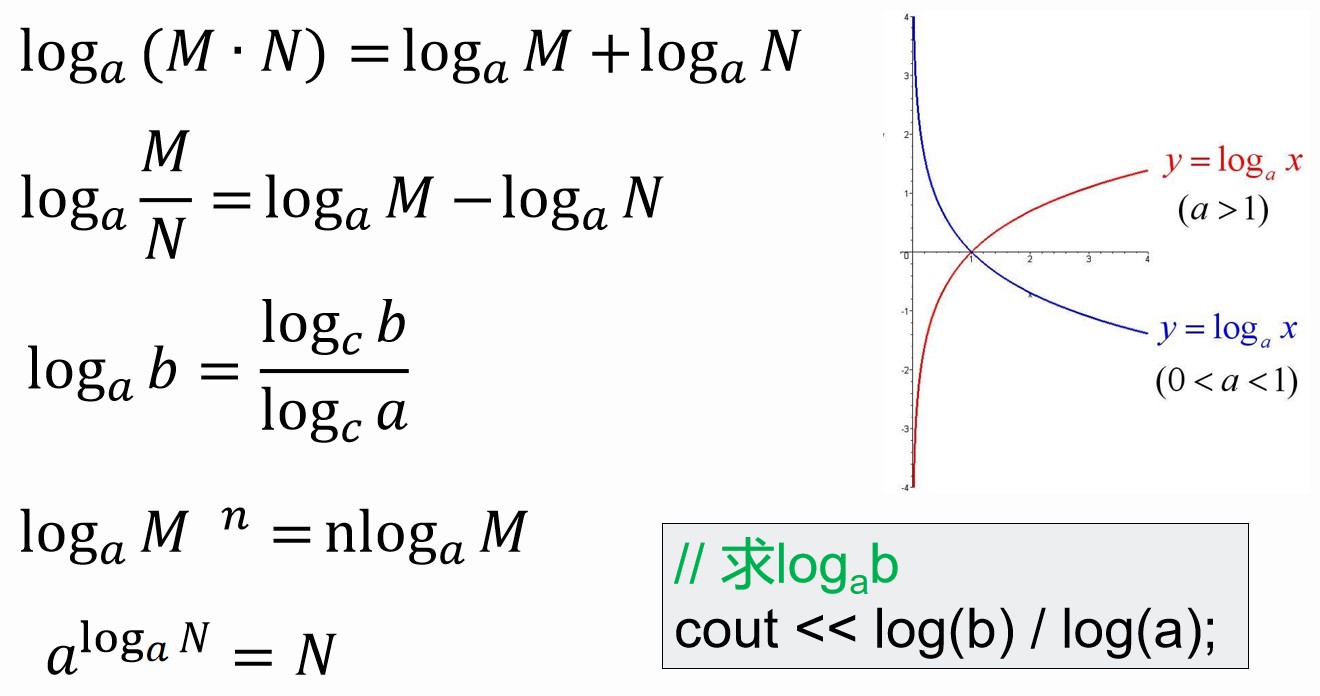
image.png

指数与对数

image.png

image.png

同余定理

同余关系

给定一个正整数m，如果两个整数a和b满足(a-b)能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)。 a≡b(mod m)，即两个整数a、b除以整数m所得的余数相等。

  • ①反身性：a ≡ a(mod m)

  • ②对称性：若 a ≡ b(mod m)，则 b ≡ a(mod m)

  • ③传递性：a ≡ b(mod m)，b ≡ c(mod m)，则 a ≡ c(mod m)

  • ④同余式相加： a ≡ b(mod m)，c ≡ d(mod m)，则 a ± c ≡ b ± d(mod m)

  • ⑤同余式相乘：a ≡ b(mod m)，c ≡ d(mod m)，则 ac ≡ bd(mod m)

  • ⑥线性运算：a ≡ b(mod m)，c ≡ d(mod m)，则 a ± c ≡ b ± d(mod m)，a * c ≡ b * d(mod m)…

同余定理加法乘法应用

  • (a + b)%m = (a%m + b%m)%m

  • (a - b)%m = (a%m - b%m)%m

  • (a * b)%m = (a%m * b%m) %m

如果只有加、减、乘运算，求结果对m取模，可以在运算的过程中让中间结果对m取模。

例：(a+b*c)%m = (a%m + (b%m * c%m)%m)%m

约数和质数

约数（又称因数）：整数a能够整除b，我们就说a是b的约数。

分解质因数：每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数。

image.png

质数（又称素数）：是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

合数：在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。

1既不属于质数也不属于合数。

最大公约数与 最小公倍数

几个自然数公有的约数，叫做这几个自然数的公约数。

公约数中最大的一个公约数，称为这几个自然数的最大公约数。

辗转相除法： 用较大数除以较小数，得到余数。 若余数为0，那么上一次除法中的除数就是最大公约数。 若余数不为0，那么下一次的除法为上一次除法中的除数除以余数。 重复这一过程，直到得到最大公约数 。

最小公倍数：两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。

若两个整数a，b的最大公约数是gcd(a,b)，最小公倍数是lcm(a,b)，那么有：

a * b = gcd(a,b) * lcm(a,b)

lcm(a,b) = a / gcd(a,b) * b