题目背景
题目描述
小明正在玩一款解谜游戏。谜题由 24 24 24 根塑料棒组成,其中黄色塑料棒 4 4 4 根,红色 8 8 8 根,绿色 12 12 12 根 (后面用 Y 表示黄色、R 表示红色、G 表示绿色)。初始时这些塑料棒排成三圈,如上图所示,外圈 12 12 12 根,中圈 8 8 8 根,内圈 4 4 4 根。
小明可以进行三种操作:
- 将三圈塑料棒都顺时针旋转一个单位。例如当前外圈从 0 0 0 点位置开始顺时针依次是
YRYGRYGRGGGG,中圈是RGRGGRRY,内圈是GGGR。那么顺时针旋转一次之后,外圈、中圈、内圈依次变为:GYRYGRYGRGGG、YRGRGGRR和RGGG。 - 将三圈塑料棒都逆时针旋转一个单位。例如当前外圈从 0 0 0 点位置开始顺时针依次是
YRYGRYGRGGGG,中圈是RGRGGRRY,内圈是GGGR。那么逆时针旋转一次之后,外圈、中圈、内圈依次变为:RYGRYGRGGGGY、GRGGRRYR和GGRG。 - 将三圈 0 0 0 点位置的塑料棒做一个轮换。具体来说:外圈 0 0 0 点塑料棒移动到内圈 0 0 0 点,内圈 0 0 0 点移动到中圈 0 0 0 点,中圈 0 0 0 点移动到外圈 0 0 0 点。例如当前外圈从 0 0 0 点位置开始顺时针依次是
YRYGRYGRGGGG,中圈是RGRGGRRY,内圈是GGGR。那么轮换一次之后,外圈、中圈、内圈依次变为:RRYGRYGRGGGG、GGRGGRRY和YGGR。
小明的目标是把所有绿色移动到外圈、所有红色移动中圈、所有黄色移动到内圈。给定初始状态,请你判断小明是否可以达成目标?
输入格式
第一行包含一个整数 T T T,代表询问的组数。 ( 1 ≤ T ≤ 100 ) (1 \le T \le 100) (1≤T≤100)。
每组询问包含 3 3 3 行:
第一行包含 12 12 12 个大写字母,代表外圈从 0 0 0 点位置开始顺时针每个塑料棒的颜色。
第二行包含 8 8 8 个大写字母,代表中圈从 0 0 0 点位置开始顺时针每个塑料棒的颜色。
第三行包含 4 4 4 个大写字母,代表内圈从 0 0 0 点位置开始顺时针每个塑料棒的颜色。
输出格式
对于每组询问,输出一行 YES 或者 NO,代表小明是否可以达成目标。
样例 #1
样例输入 #1
2
GYGGGGGGGGGG
RGRRRRRR
YRYY
YGGGRRRRGGGY
YGGGRRRR
YGGG
样例输出 #1
YES
NO
提示
蓝桥杯 2019 年国赛 B 组 H 题。
1、题目分析
(1)它有三种移动方式,其中第一种和第二种是类似的,是不将颜色块所属的圈子更换的,就只是同时顺时针和逆时针,同时我们可以发现,外圈有12个,中圈8个,内圈4个。也就是说,同时顺时针和逆时针旋转的时候,内圈的颜色块是固定的对应中圈的两个颜色块和外圈的三个颜色块。如图所示:
起始状态,外1,中1和内1是对应的。
顺转4次后,外3,中2和内1是对应的;
再顺转4次后,外2,中1和内1是对应的;
再顺转4次,外1,中2和内1是对应的;
再顺转4次,外3,中1和内1是对应的;
再顺转4次,外2,中2和内1是对应的;
也就是说,在不更改颜色块的圈子的操作中,内1个、中2个和外3个是固定搭配的,无论怎么操作顺逆时针,都是固定的。这六个颜色块:外1、2、3、中1、2、内1无法和其他的颜色块交换。
外1,中1,内1;√
外1,中2,内1;√
外2,中1,内1;√
外2,中2,内1;√
外3,中1,内1;√
外3,中2,内1;√
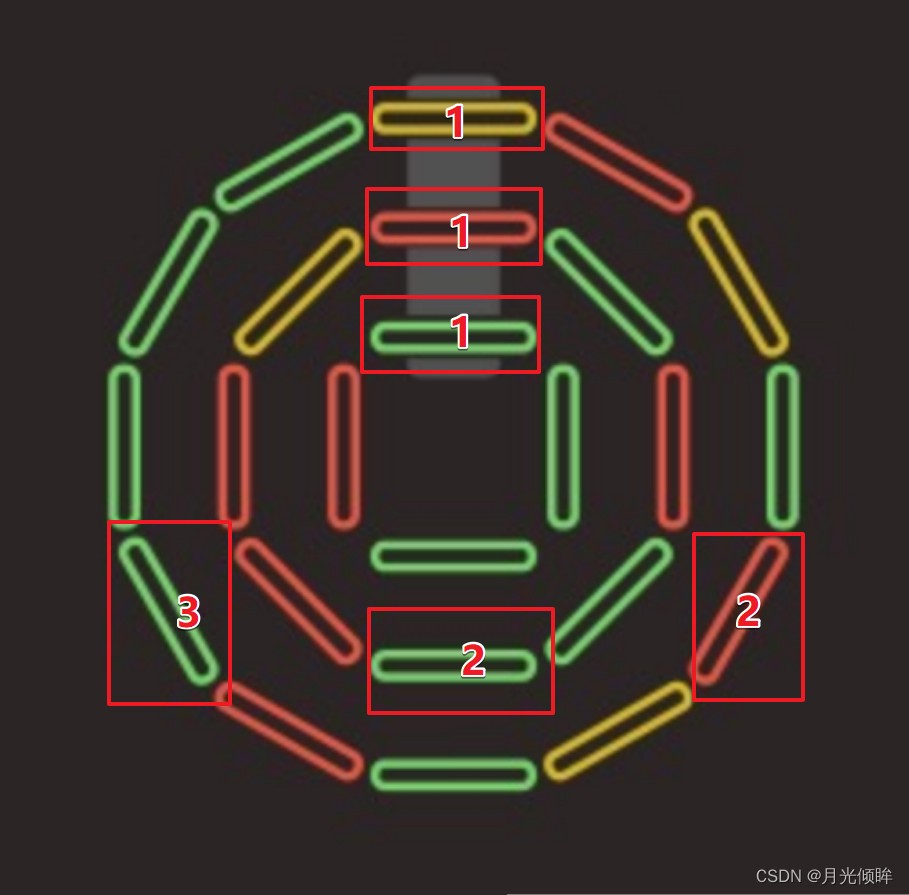
(2)第三种移动方式,以目前的图中情况为例:可以将内1换到中1和外1的任意位置;同理也可以把中1换到内1和外1的任意位置;可以把外1换到内1和中1的任意位置。
(3)也就是说,可以将12,8,4的搭配,拆分为4组3,2,1的搭配。判断这四组是不是都可以满足3G,2R,1Y的搭配数量,就可以判断整体的情况了。
2、代码思路
使用三个桶统计每一组的三色数量,然后判定数量是否是3,2,1。
3、代码
#include<iostream>
#include <cstring>
#include <vector>
#include <map>
using namespace std;
int main()
{
int n;cin>>n;//需要我们判断多少次
while(n--)
{
bool flag=true;
string in_color,mid_color,out_color;
cin>>out_color>>mid_color>>in_color;
for(int i=0;i<4;i++)
//每次都需要拆分为4组来判断
{
map<char,int>color;//储存颜色数量
//内圈
color[in_color[i]]++;
//中圈
color[mid_color[i]]++;
color[mid_color[i+4]]++;
//外圈
color[out_color[i]]++;
color[out_color[i+4]]++;
color[out_color[i+8]]++;
//只要有一个颜色的数量不对,那么就说明不能完成,将flag置为false,并且跳出循环
if(color['Y']!=1||color['R']!=2||color['G']!=3)
{
flag=false;
break;
}
}
//输出结果
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}