第9关 - 2017佛山图书馆GoC决赛试题
173.(佛山图书馆GoC决赛试题 )第1题:五个方形(five)
题目描述
小P刚学会goc时最喜画正方形拼成的图形,请编程画出如下图形。
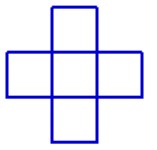
注意:上图的每个线段长度都是50。
题解
这道题主要考查图形分解,最简洁的是看到两个长方型旋转叠加。。
也可以成 4 个正方形 ,围绕中间的正方型旋转。
int main(){
p.r(150,50,2).r(50,150,2);
return 0;
}
174.(佛山图书馆GoC决赛试题 )第2题 眼镜(glasses)
题目描述
小P设计了如下图的“眼镜”,请你帮忙使用GoC编程绘制。
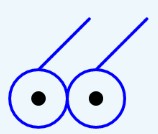
注意:眼镜黑心圆半径为10,外圆半径为40,眼镜架长度100、斜了45度。
题解
int main(){
p.up()
.o(40,2).oo(10,0)
.fd(40)
.down()
.rt(45).fd(100);
p.moveTo(80,0)
.up().lt(45)
.o(40,2).oo(10,0)
.fd(40)
.down()
.rt(45).fd(100);
return 0;
}
175.(佛山图书馆GoC决赛试题 )第3题:小树(tree)
题目描述
小P现在学会使用颜色命令,他使用2种新的颜色:棕色(6号)和绿色(3号)设计了如下图的“小树”,当然为了可变,图中正三角形的个数n和线段长度a是输入的,请你帮忙使用GoC编程绘制。
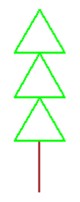
注意:所有线段长度都一样。
输入格式 一行:2个正整数n和a。
输出格式 相应的图形。
输入/输出例子1
输入:
1 50
输出:
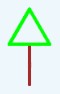
输入/输出例子2
输入:
5 20
输出:

题解
int main(){
int n,a;
cin >> n>>a;
p.c(6).fd(a);
p.c(3).rt(90);
for(int i=1;i<=n;i++){
p.bk(a/2.0);
for(int j= 1;j<=3;j++){
p.fd(a).lt(120);
}
// 返回三角形顶点
p.rt(120).bk(a).lt(120);
}
return 0;
}
176.(佛山图书馆GoC决赛试题 )第4题:雪花(snow)
题目描述
小pen正在研究一种特殊的雪花:
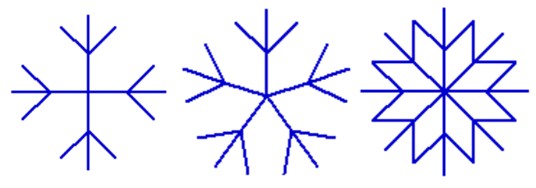
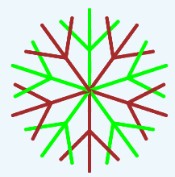
研究发现,它们都是由一些边长为30 的小“叉”组成的,第1个图有4个小叉,第2个图有5个小叉,第3个图有8个小叉。 小pen浪浪的想,不仅要有不同的小叉个数,还应该配上2种颜色间隔的画才好看。比如输入小叉个数n=6,两种颜色号a=3、b=4,画出的图如下:

注意:所有线段长度都一样为50。
输入格式 一行:3个正整数n和a、b。
输出格式 相应的图形。
输入/输出例子1
输入:
10 3 6
输出:
输入/输出例子2
输入:
16 9 11
输出:

题解
int main(){
int n,a,b;
cin >> n >> a >> b;
for(int i=0;i<n;i++){
if(i%2==0) p.c(a);
else p.c(b);
p.fd(50).lt(45).fd(50).bk(50)
.rt(90).fd(50).bk(50).lt(45)
.fd(50).bk(100);
p.rt(360.0/n);
}
return 0;
}
177.(佛山图书馆GoC决赛试题 )第5题 同心圆(cir)
题目描述
小Pen上数学辅导课,内容是等差数列,就是一系列数,每相邻的2项之间的差都相等(后项-前项)。 比如下面三个数列都是等差数列: 1 2 3 4 5 6….; 10 13 16 19 22….; 100 95 90 85 80 …. 小Pen一听就“秒懂”了,无聊时他就喜欢画100个同心圆,第1个圆半径是1,第2个圆半径是2,第3个圆半径是3,….。结果如下图:

这时数学老师提问,如果给定等差数列的第1项和第100项,你能不能写出所有的中间项?小Pen瞬间有了联想:能不能用100个圆来表示这100项数列呢? 就用等差数列的数值当颜色的RGB值!数列的第1项当半径为1圆的颜色RGB、数列的第2项当半径为2圆的颜色RGB、数列的第3项当半径为3圆的颜色RGB、…。
- 提示:RGB值x变为goc的颜色命令为:pen.rgb(x%256, x/256%256, x/256/256).c(16);
例如:第1项是50,第100项是248,画出的是:

输入格式 一行2个正整数a,b范围[1,10000000]。a表示数列的第1项,b表示数列的第100项。
输出格式 相应的图形。
输入/输出例子1
输入:
500 104
输出:

输入/输出例子2
输入:
500000 500297
输出:

题解
方法一:从里向外画圆
int main(){
int n,a,b,d;
cin >> a >> b;
n= 100;
// 计算每个间隔的距离
d=(b-a)/(n-1);
for(int i=1;i<=n;i++){
p.rgb(a%256,a/256%256,a/256/256).c(16);
p.o(i);
a+=d;
}
return 0;
}
方法二:从外向里画圆
int main(){
int n,a,b,d;
cin >> a >> b;
n= 100;
d=(b-a)/(n-1);
p.speed(1);
while(n--){
p.rgb(b%256,b/256%256,b/256/256).c(16);
p.o(n);
b -=d;
}
return 0;
}
178.(佛山图书馆GoC决赛试题 )第6题:靠近(close)
题目描述
小pen有4个正方形,1个红色(1号颜色)正方形、1个黑色(0号颜色)正方形、1个紫色(11号颜色)正方形和1个绿色(10号颜色)正方形,他把红色放在上面黑色放在下面对齐组成左边一对,把紫色放在上面绿色放在下面对齐组成右边一对,两个的下面都在“地面上”。例如下图是4个边长分别是40 20 30 60的情况下画出的图形:

现在,小pen想让左右两对图形不改变形状的前提下尽量靠近,例如上面的图靠近后就变为:

输入格式 一行4个正整数a、b、c、d,范围都在[10,100]。分别表示红色正方形、黑色正方形、紫色正方形和绿色正方形的边长。
输出格式 相应的图形。
输入/输出例子1
输入:
70 50 20 10
输出:

输入/输出例子2
输入:
50 30 20 28
输出:

题解
方法一:
int a,b,c,d;
int pdL() //计算绿色能靠近多少
{
int min=b/2;
if ( d>b && a>b){ // D高了
min=a/2;
}
min += d / 2;
cout << min;
return min;
}
int pdR() // //计算紫色能靠近多少
{
int min = b / 2;
if (d >= b && d < a + b)
min = a / 2;
else if (d < b && c + d > b && a > b)
min = a / 2;
min += c / 2;
cout << min;
return min;
}
int main()
{
cin >>a>>b>>c>>d;
p.up()
.fd(b/2).rr(b,b,0)
.fd(b/2+a/2).rr(a,a,1);
int xx=pdL();
int yy=pdR();
if (xx<yy) xx=yy;
p.moveTo( xx ,0)
.fd(d/2).rr(d,d,10)
.fd(d/2+c/2).rr(c,c,11);
return 0;
}
方法二:
int a,b,c,d;
void draw(int a,int b,int c1, int c2) //画一对
{
p.up()
.fd(b/2). down()
.rr(b,b,c1).up()
.fd(b/2+a/2).down()
.rr(a,a,c2).up()
.bk(a/2+b);
}
int pd1() //计算绿色能靠近多少
{
int min=b/2;
if ( d>b ) //d高了
{
if (a>b) min=a/2;
}
cout << min+d/2;
return min+d/2;
}
int pd2() //计算紫色能靠近多少
{
int min=0;
if ( d<b ) //d矮了
{
min=b/2;
if ( c+d>b) //也碰到红色的
if (a>b) min =a/2;
}
else
{
if (d <a+b)
min=a/2;
}
cout << min+c/2;
return min+c/2;
}
int main()
{
cin >>a>>b>>c>>d;
draw(a,b,0,1);
int xx=pd1();
int yy=pd2();
if (xx<yy) xx=yy;
p.moveTo( xx ,0);
draw(c,d,10,11);
return 0;
}







